こんにちは!セイジュン@ITストラテジストです。社会に出て30年弱、もともとは文系出身ですが、プログラマからシステムエンジニア、プロジェクトマネージャとして生きてきました。その中で、最も利用した数式・公式が「内項の積は外項の積に等しい」です。
社会に出て30年弱その中で、最も利用した数式・公式が「内項の積は外項の積に等しい」です。
内項の積は外項の積に等しい
A:B = C:D
これは比例を表す数式、比例式と呼ばれています。
比例式には「内項 (B と C) の積(掛け算)は外項(A と D) の積に等しい」という性質があります。
この公式が、本日のテーマです。
具体的に数字を置いてみましょう。
2:3=8:12
で確かめてみると、内項の積は3×8=24。外項の積は2×12=24で等しくなります。
これ、中学1年生の数学で習うそうです。
一応、念のため証明です。
大丈夫ですかね。。。
では、次の問題を解いてみましょう。
公式に当てはめてみましょう。
3:2=15:x
内項の積は外項の積に等しいので、
2×15=3×X
3X=2×15
X=30/3
X=10 よって、B社の売上は10億円
二つのものを比較して 仮説を立てる
なぜ、この数式・公式が役に立つのでしょうか?
それは、二つのものを比べて仮説を立てる時に最適だからです。
「二つのものを比べる」とは、上記のように A 社 B 社(通常は自社とコンペティター)といった二つの実態に対する比較であったり、昨年度の実績と今年度の計画という二つの時間に対する比較だったりします。
「仮説を立てる」というのは、 A・B・C・D のうち三つが特定できれば残りの一つが仮置き出来るということを指します。
ちょっと回りくどい言い方になってきたので、私が社会人になってからの役割の変遷に従って具体例を見てみましょう。
プログラマー時代
プログラムを組んでいると、完成までの計画立てが必要になります。
例えば、
前回のプログラミングの際は1,000ステップのプログラムをコーディングからコンパイルチェック、テストまで一週間かかった。ということは、今回のプログラムは難易度から2,500ステップ相当だから2週間半だな。
と計画立てしますね。これは、誰もがすることであり、直感でやっていますが
1,000:5 = 2,500: X
を考えたわけです。
システムエンジニア時代
システムエンジニア時代であれば、例えば
テスト工程であぶり出したいバグ(不具合)をシミュレーションするために、前回のテストではプログラム80本でバグ240件、抽出できた。ということは、今回は100本なので何件をチェックポイントにテストをやっていけばいいのかな。
数式にあてはめてみると、以下ですね。
80:240=100:X
X=300
プロジェクトマネージャ時代
プロマネの時であれば、例えば
プロジェクト完成まで全体で12か月って計画していて、今計画対比で進捗率60%。で、今9か月目か。。。どのくらいヤバいんだっけ。
12:9=100:X
X=75
つまり、本当は75%進捗していたかった。。。現実は60%。つまり15%遅延!
ITストラテジスト時代
三つの事象の比較にも使います。
お客様企業のIT投資なんだけど、前期は総費用1.2億円のうちAシステムに8千万、Bシステムに3千万、Cシステムに1千万投下したんだ。比率は、、、
12:100=8:A ・・・A=67%
12:100=3:B ・・・B=25%
12:100=1:C ・・・C=8%
とした場合、今期はどうする?このままの比率を継続するのか、むしろ投下比率を変えるのか、お客様と議論だな。
といった具合です。
事例は非常に単純化していますが、これの複雑バージョンを社会人の皆さんは直観的にこなしているということではないでしょうか。
もう一度いいますね。
「内項の積は外項の積に等しい」
これ、大事です。
「内項の積は外項の積に等しい」が通じない世界
「内項の積は外項の積に等しい」
この数式は、比例式なので書いてみればリニアな曲線。非常に分かりやすいものです。
とはいえ、この数式(あるいはグラフ)が万全でないのも、また事実です。
そして、そのことは社会人の皆さんも知っています。
代表的なものを2つ。一つはエンジニアリングの分野から、もう一つは世の中全体のこと、です。
とくに二つ目は今までのちゃぶ台返し的なことではありますが、どちらの考え方も有効だと認識したいところです。
バスタブ曲線
バスタブ曲線は、故障率曲線が正式名称。
故障率曲線(こしょうりつきょくせん)とは、機械や装置の時間経過tに伴う故障率y (t) の変化を表示した曲線のこと。時間の経過により初期故障期、偶発故障期、摩耗故障期の3つに分けられる。 ~Wikiより
こんな曲線です。
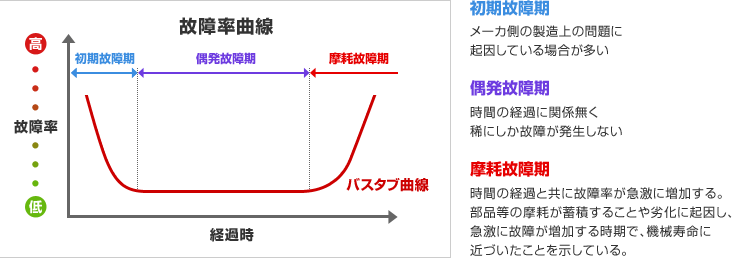
アイダエンジニアリング(株)様サイトより引用させて頂きました
これ、エンジニアの方でなくても肌感覚で分かると思います。つまり、製品は初期不良が、ある一定数出て、その後は安定的に使えて、最後は経年劣化で故障率があがるというアレです。
先ほどのITストラテジストの時代は、こんな数字も見ながら投資計画を作っていました。余談ですが。
ロングテール
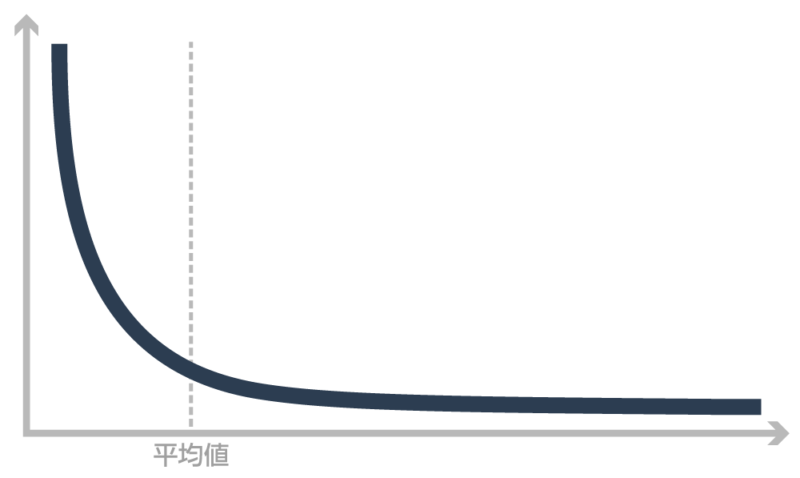
これも昨今言われることです。
世の中は、リニア、直線で示されると思いすぎてはいけないのですね。ロングテールの先には不確実な事象・世界が待っています。
比例式、比例のグラフのように、去年と比べて今年、その延長での来年/他社と比べて当社、こういう比較と仮説はモチロン役にたつのですが、最近良く会社でも「思いっきり振った話として、、」なども言われます。
あるいは、プライベートでも他者と比べて自分、を考えすぎることは人生をつまらなくることでもあると思います。
今までのちゃぶ台返し的なことではありますが、
比例式=相似として予測可能な未来
ロングテール=不確実な未来
どちらの考え方も有効だと認識したいところです。
ではまた。